Multiparametrical optimization
While solving research problems connected to
searching optimal combinations of several engine parameters, such as compression ratio,
injection timing, diameter, number and direction of injector nuzzles, combustion chamber
shape, valve timing, turbocharging parameters etc., it can be hard to plan and treat with
a numerical experiment with many variable factors. Very effective here is
multiparametrical optimization, when searching of optimal combination of variable factors
is laid on the formal procedure of non-linear programming, and the researcher only has to
formulate the optimal search problem correctly and analyze obtained solution. Optimal
search procedures during searching an extremum of a multiparametrical function use the
super- or turbocharged engine mathematical model to connect independent variables
(optimization parameters) with the goal function and with restrictions.
Goal function
Parameters of efficiency of an engine or its separate
processes can be included in a goal function:
Zj = Zj (Xk).
The finding of an extremum of a goal function is a problem of
optimization.
Vector of explanatory variables
Vector of explanatory variables Xk is a
set of design data of an engine. At the expense of selection of value of these data is
planned to achieve an extremum of a goal function.
Restrictions
As a rule at a searching of optimum combination
of ICE design data it is necessary to monitor engine thermal and mechanical
tensions, emission level and other monitoring factors which limit area of optimum
searching and are the restrictions. The restraining parameters, as well as a goal function
depend on explanatory variables:
Yi = Yi (Xk).
The analytical relation between a goal function both
restrictions on the one hand and vector of explanatory variables on the other hand does
not exist, therefore for their calculation the mathematical model of ICE is used.
Thus, the problem of optimization of an engine is reduced to a
problem of non-linear programming, i.e. to a problem of searching of an optimum of a
function Zj (Xk) at presence of limitations: Yi
min < Yi (Xk) < Y i max.
The presence of restrictions essentially complicates a solution of
optimization problems, therefore it is expedient to reduce a problem of conditional
optimization to a problem of non-conditional optimization, the algorithms for which much
better designed. Method of penal functions is an effective mode to take into account of
restrictions. The essence of a method is, that at violation of restriction to a minimized
goal function the penalty is added. The penalty will increase in accordance with
magnification of violation of restriction. Generally the goal function is a sum of three
items. Each item has its influence coefficient Czj, Cyi, Cxk.
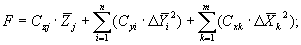
where: Czj |
is a line factor (influence coefficient) of optimized ICE
parameter Zj included into goal function;
|
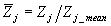
|
is a relative ICE parameter Zj related to
its mean average value (for example: sfc, power, NO emission, etc.);
|
Cyi
|
is a penal factor for leaving permitted area of Yi; |
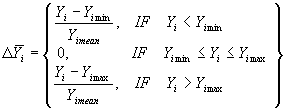 |
is a related value of violation of restriction Yi; |
Cxk
|
is a penal factor for leaving permitted area of Xk ;
|
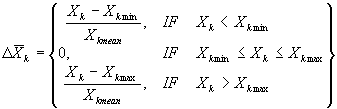 |
is a related value of Xk lapped over
allowable borders; |
Mean values of explanatory variables Xk mean
and restrictions Yi mean as well as penal factors of
Xk are set by program.
Specification of penal factors for restrictions Cyi
; max. and min. borders for restrictions Yi min , Yi
max and explanatory variables Xi min , Xi
max as well as goal function Zj has to be made by user in
preprocessor of DIESEL-RK.
Library of algorithms of DIESEL-RK software
For searching an extremum of function of many variables
the well known algorithms of nonlinear programming are used.
Non-linear programming theory doesn't say which methods
are better so while selecting these methods the researcher should be guided by his own
experience of optimization problems salvation.
DIESEL-RK library contains 14 algorithms:
Zero-order methods don't use partial derivatives of goal function:
- On-coordinates descent method.
- "Deformable polyhedron" method by Nelder and Mead.
- Rosenbrok method.
- Powell method.
First-order methods use partial derivatives of goal function:
- "Quickest descent" method.
- "Heavy ball" method.
- Flatcher-Reeves method.
- Polak-Ribier method.
- Projective method of Newton-Rafson.
- Davidon-Flatcher-Powell method.
- Broiden method (rank 1).
- Pearson method 2.
- Pearson method 3.
Random search method:
Monte-Carlo method.
All algorithms provide finding solutions of optimization
problems with different efficiency. DIESEL-RK developers can only advise to use
first-order methods in the cases when expected optimum is far from the starting point.
Methods of quickest descent and heavy ball also give good results.
The great many of methods is necessary for checkout of the
obtained solutions. If the solutions obtained by different methods are similar, there is
greater reliance that the obtained solution is really optimal.
Usage of the optimization program is especially effective at
solving the problems of engine boosting, at development of new constructions, and also at
modernization directed on decrease of fuel consumption and emission of harmful materials.
Example of usage of the optimization is represented in
page:
Multiparametric
optimization of a medium-speed marine diesel at increase its capacity.
Bibliography
- Hooke R., Jeeves T.A. Direct Search Solution of Numerical and Statistical Problems. S.
Assoc. Computer. Mach. 8,1962, pp.212- 229.
- Nelder J.A., Mead R. Computer J., 7, 1964, pp.368.
- Rosenbrok H.H. Computer J., 3,1960, pp.175.
- Powell M.J.D. Computer J., 7,1964, pp.155; 7,1965, pp.303.
- Pearson J.D. Computer J., 13,1969, pp.171.
- Flatcher R., Powell M.J.D. Computer J., 6,1963, pp.163-168.
- Flatcher R., Reeves C.M. Computer J., 7,1964, pp.149.
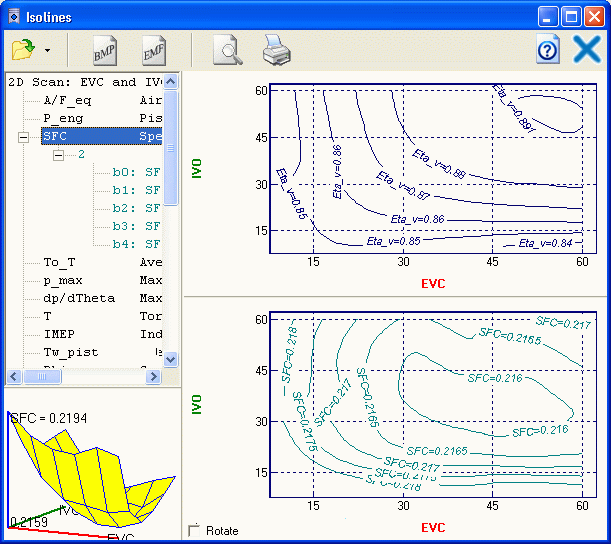
Scanning
If an optimization problem can be formulated as a
2D-problem (number of variables = 2), it is optimal to use scanning, when engine
parameters are calculated in the nods of an orthogonal grid, where X-axis is used for the
first parameter and Y-axis - for the second parameter. Scanning results are used to build
surfaces, where many parameters can be displayed in form which can be used for analysis:
- 3D graph of a function of two arguments,
- isoline family (sections of these surfaces at different function levels).
Example:
2D scanning results are displayed as surface plot and isoline
families.
SFC and volumetric efficiency of four-stroke diesel as functions of gas exchange timing:
EVC and IVO.
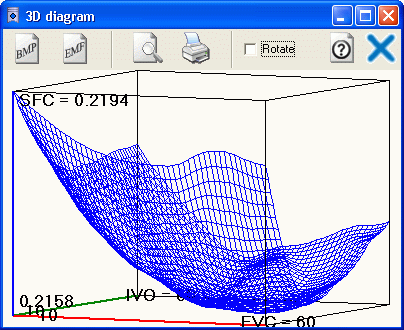
Enlarged 3D diagram.
Use of the scanning allows fast finding the effective
decisions at development of engines.
To home page






|



